[Algorithm] ZUC —— “祖冲之”流密钥算法的代码解释

ZUC算法分析

本文写于作者进行密码学课程实验过程中，会以“初学者”的视角去解读。不涉及CTF中的逆向、密码知识，只为做深入理解并为后面复习所用。文章代码源于AI生成，作者专门调过提示词，按照GB/T33133.1—2016标准设计，可能与其他标准或实现顺序有区别，如有问题，请联系作者：（后面开个仓库）

前言

首先，想了解ZUC算法是什么：祖冲之算法，也称为ZUC算法，是一种由中国学者自主设计的同步序列密码算法（流密码），主要用于加密和数据完整性校验。它是中国第一个成为国际密码标准的算法，被采纳为4G移动通信系统（LTE）的国际标准...

以下是GB/T33133.1—2016标准中的算法结构图：

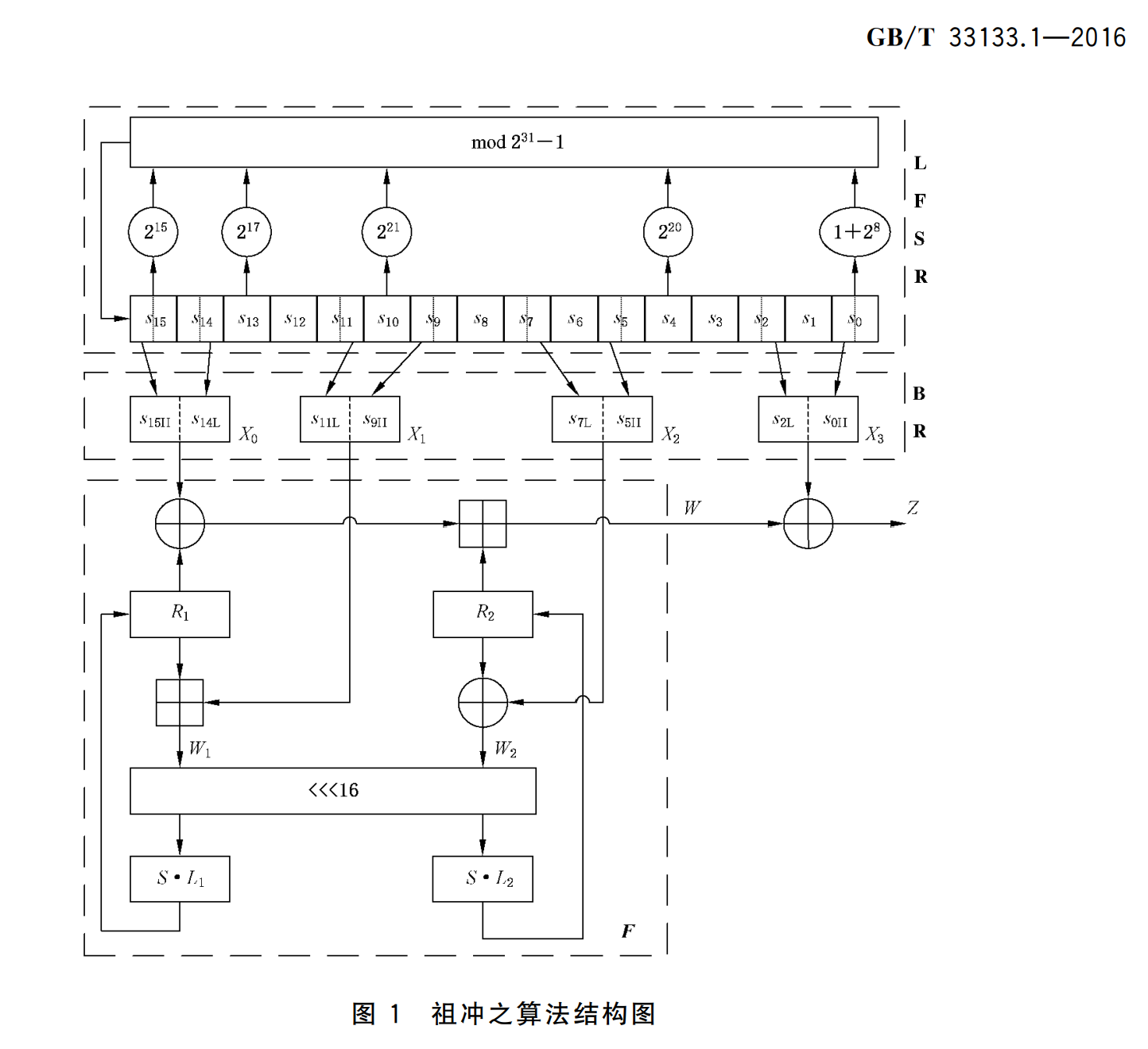
现在看不懂还很正常，下面我们会结合代码一层层地解释。简单来说，ZUC算法是一种可以用于生成 流密钥的算法，用于 流密码加密，其核心有三个步骤

• 比特重组(BR)
• 非线性函数F(F)
• 线性反馈移位寄存器(LFSR)

代码实现上，还需考虑预处理一下输入

• 预处理

而得到的 流密钥用于加密解密只需要简单异或一下就行了

• 加密解密

综上，本文将分为以上5部分去尽可能完整且详细地介绍ZUC算法

PS：本文将以递进式的方式去介绍，而不是分块式，建议跟着一步步看，不然容易出现思维跳跃

（以下是程序源码：）

############## ZUC密钥生成算法实现 ##############
class ZUCAlgorithm:

    def __init__(self, key, iv):
        """
        初始化ZUC算法
        :param key: 128位初始密钥 (16字节)
        :param iv: 128位初始向量 (16字节)
        """
        print("=== ZUC算法初始化开始 ===")
  
        # LFSR: 16个31位寄存器
        self.LFSR = [0] * 16
  
        # 非线性函数F的记忆单元
        self.R1 = 0
        self.R2 = 0
  
        self.key = key
        self.iv = iv
  
        print(f"密钥: {key.hex()}")
        print(f"初始向量: {iv.hex()}")
  
        # 初始化常量
        self.d = self._init_d_constants()
        self.sbox = ZUCSBox()
  
        print("=== ZUC算法初始化完成 ===\n")
  
    def _init_d_constants(self):
        """初始化15位常量d_i"""
        print("步骤: 初始化15位常量d_i")
        d_values = [
            0b100010011010111, 0b010011010111100, 0b110001001101011,
            0b001001101011110, 0b101011110001001, 0b011010111100010,
            0b111000100110101, 0b000100110101111, 0b100110101111000,
            0b010111100010011, 0b110101111000100, 0b001101011110001,
            0b101111000100110, 0b011110001001101, 0b111100010011010,
            0b100011110101100
        ]
        return d_values
  
    def key_load(self):
        """
        将初始密钥k和初始向量iv装入到LFSR的寄存器单元变量中
        """
        print("=== 密钥装入过程开始 ===")
  
        for i in range(16): # ①确保每个寄存器都包含了密钥、固定值和初始向量的信息
            # 提取密钥和初始向量的字节
            k_byte = self.key[i]
            iv_byte = self.iv[i]
  
            # s_i = k_i || d_i || iv_i
            # k_i: 8位, d_i: 15位, iv_i: 8位
            self.LFSR[i] = (k_byte << 23) | (self.d[i] << 8) | iv_byte
  
            print(f"LFSR[{i}] = {self.LFSR[i]:08x} (k={k_byte:02x}, d={self.d[i]:04x}, iv={iv_byte:02x})")
  
        print("=== 密钥装入过程完成 ===\n")
  
    def mod_231_1_add(self, a, b):
        """
        模2^31-1加法实现
        """
        result = a + b
        result = (result & 0x7FFFFFFF) + (result >> 31)
        return result
  
    def mod_231_1_mult(self, a, b):
        """
        模2^31-1乘法实现
        """
        return (a * b) % (2**31 - 1)
  
    def lfsr_initialization_mode(self, u):
        """
        LFSR接收1个31比特字u的输入，更新寄存器
        """
        # (1) 计算v
        v = self.mod_231_1_mult(2**15, self.LFSR[15])
        v = self.mod_231_1_add(v, self.mod_231_1_mult(2**17, self.LFSR[13]))
        v = self.mod_231_1_add(v, self.mod_231_1_mult(2**21, self.LFSR[10]))
        v = self.mod_231_1_add(v, self.mod_231_1_mult(2**20, self.LFSR[4]))
        v = self.mod_231_1_add(v, self.mod_231_1_mult((1 + 2**8), self.LFSR[0]))
  
        # (2) 计算s16
        s16 = self.mod_231_1_add(v, u)
  
        # (3) 如果s16=0，则置s16=2^31-1
        if s16 == 0:
            s16 = 2**31 - 1
  
        # (4) 移位操作
        for i in range(15):
            self.LFSR[i] = self.LFSR[i + 1]
        self.LFSR[15] = s16
  
        return s16
  
    def lfsr_work_mode(self):
        """
        LFSR工作模式
        LFSR无输入，直接更新寄存器
        """
        # (1) 计算s16
        s16 = self.mod_231_1_mult(2**15, self.LFSR[15])
        s16 = self.mod_231_1_add(s16, self.mod_231_1_mult(2**17, self.LFSR[13]))
        s16 = self.mod_231_1_add(s16, self.mod_231_1_mult(2**21, self.LFSR[10]))
        s16 = self.mod_231_1_add(s16, self.mod_231_1_mult(2**20, self.LFSR[4]))
        s16 = self.mod_231_1_add(s16, self.mod_231_1_mult((1 + 2**8), self.LFSR[0]))
  
        # (2) 如果s16=0，则置s16=2^31-1
        if s16 == 0:
            s16 = 2**31 - 1
  
        # (3) 移位操作
        for i in range(15):
            self.LFSR[i] = self.LFSR[i + 1]
        self.LFSR[15] = s16
  
        return s16
  
    def bit_reconstruction(self):
        """
        比特重组(BR)
        从LFSR寄存器中重组4个32位字X0, X1, X2, X3
        """
        # 提取LFSR寄存器的高16位和低16位
        s15H = (self.LFSR[15] >> 15) & 0xFFFF  # s15的高16位
        s14L = self.LFSR[14] & 0x7FFF          # s14的低15位
        s11H = (self.LFSR[11] >> 15) & 0xFFFF  # s11的高16位
        s9L = self.LFSR[9] & 0x7FFF            # s9的低15位
        s7H = (self.LFSR[7] >> 15) & 0xFFFF    # s7的高16位
        s5L = self.LFSR[5] & 0x7FFF            # s5的低15位
        s2H = (self.LFSR[2] >> 15) & 0xFFFF    # s2的高16位
        s0L = self.LFSR[0] & 0x7FFF            # s0的低15位
  
        # 重组32位字
        X0 = (s15H << 16) | s14L
        X1 = (s11H << 16) | s9L
        X2 = (s7H << 16) | s5L
        X3 = (s2H << 16) | s0L
  
        return X0, X1, X2, X3
  
    def linear_transform_L1(self, X):
        """
        线性变换L1
        L1(X) = X ⊕ (X <<< 2) ⊕ (X <<< 10) ⊕ (X <<< 18) ⊕ (X <<< 24)
        """
        def rotate_left_32(x, n):
            """32位循环左移"""
            return ((x << n) | (x >> (32 - n))) & 0xFFFFFFFF
  
        result = X
        result ^= rotate_left_32(X, 2)
        result ^= rotate_left_32(X, 10)
        result ^= rotate_left_32(X, 18)
        result ^= rotate_left_32(X, 24)
  
        return result & 0xFFFFFFFF
  
    def linear_transform_L2(self, X):
        """
        线性变换L2
        L2(X) = X ⊕ (X <<< 8) ⊕ (X <<< 14) ⊕ (X <<< 22) ⊕ (X <<< 30)
        """
        def rotate_left_32(x, n):
            """32位循环左移"""
            return ((x << n) | (x >> (32 - n))) & 0xFFFFFFFF
  
        result = X
        result ^= rotate_left_32(X, 8)
        result ^= rotate_left_32(X, 14)
        result ^= rotate_left_32(X, 22)
        result ^= rotate_left_32(X, 30)
  
        return result & 0xFFFFFFFF
  
    def nonlinear_function_F(self, X0, X1, X2):
        """
        非线性函数F
        输入: X0, X1, X2 (32位字)
        输出: W (32位字)
        """
        # (1) W = (X0 ⊕ R1) + R2 mod 2^32
        W = ((X0 ^ self.R1) + self.R2) & 0xFFFFFFFF
  
        # (2) W1 = R1 + X1 mod 2^32
        W1 = (self.R1 + X1) & 0xFFFFFFFF
  
        # (3) W2 = R2 ⊕ X2
        W2 = self.R2 ^ X2
  
        # (4) R1 = S[L1(W1H || W2L)]
        W1H = (W1 >> 16) & 0xFFFF  # W1的高16位
        W2L = W2 & 0xFFFF          # W2的低16位
        R1_input = (W1H << 16) | W2L
        self.R1 = self.sbox.sbox_32(self.linear_transform_L1(R1_input))
  
        # (5) R2 = S[L2(W2H || W1L)]
        W2H = (W2 >> 16) & 0xFFFF  # W2的高16位
        W1L = W1 & 0xFFFF          # W1的低16位
        R2_input = (W2H << 16) | W1L
        self.R2 = self.sbox.sbox_32(self.linear_transform_L2(R2_input))
  
        return W
  
    def initialization_phase(self):
        """
        初始化步骤
        """
        print("=== 初始化步骤开始 ===")
  
        # (a) 密钥装入
        print("步骤(a): 密钥装入")
        self.key_load()
  
        # (b) 初始化R1和R2为0
        print("步骤(b): 初始化R1和R2为0")
        self.R1 = 0
        self.R2 = 0
  
        # (c) 重复执行32次
        print("步骤(c): 执行32轮初始化")
        for i in range(32):
            print(f"  第{i+1}轮初始化:")
  
            # 1) 比特重组
            X0, X1, X2, X3 = self.bit_reconstruction()
            print(f"    比特重组: X0={X0:08x}, X1={X1:08x}, X2={X2:08x}, X3={X3:08x}")
  
            # 2) 非线性函数F
            W = self.nonlinear_function_F(X0, X1, X2)
            print(f"    非线性函数F: W={W:08x}, R1={self.R1:08x}, R2={self.R2:08x}")
  
            # 3) 输出W (在初始化阶段通常不输出)
  
            # 4) LFSR初始化模式，输入W>>1 (取31位)
            u = W >> 1
            self.lfsr_initialization_mode(u)
            print(f"    LFSR更新: u={u:08x}")
  
        print("=== 初始化步骤完成 ===\n")
  
    def generate_keystream(self, L):
        """
        工作步骤
        生成L个32位密钥字
        :param L: 需要生成的密钥字数量
        :return: 密钥字列表
        """
        print("=== 工作步骤开始 ===")
        print(f"目标: 生成{L}个32位密钥字")
  
        keystream = []
  
        print("步骤(a): 工作阶段初始化")
        X0, X1, X2, X3 = self.bit_reconstruction()
        print(f"  比特重组: X0={X0:08x}, X1={X1:08x}, X2={X2:08x}, X3={X3:08x}")
  
        self.nonlinear_function_F(X0, X1, X2)
        print(f"  非线性函数F: R1={self.R1:08x}, R2={self.R2:08x}")
  
        self.lfsr_work_mode()
        print("  LFSR工作模式更新完成")
  
        # (b) 重复计算L次
        print(f"步骤(b): 生成{L}个密钥字")
        for i in range(L):
            print(f"  第{i+1}个密钥字生成:")
  
            # 1) 比特重组
            X0, X1, X2, X3 = self.bit_reconstruction()
            print(f"    比特重组: X0={X0:08x}, X1={X1:08x}, X2={X2:08x}, X3={X3:08x}")
  
            # 2) Z = F(X0,X1,X2) ⊕ X3
            F_output = self.nonlinear_function_F(X0, X1, X2)
            Z = F_output ^ X3
            print(f"    密钥字计算: F={F_output:08x}, Z=F⊕X3={Z:08x}")
  
            # 3) 输出密钥字Z
            keystream.append(Z)
  
            # 4) LFSR工作模式
            self.lfsr_work_mode()
            print(f"    LFSR工作模式更新完成")
  
        print("=== 工作步骤完成 ===\n")
        return keystream

############## Sbox初始化 ##############
class ZUCSBox:
    """
    ZUC算法S盒实现
    """
  
    def __init__(self):
        print("初始化ZUC S盒...")
        self.S0 = self._create_s0()
        self.S1 = self._create_s1()
  
    def _create_s0(self):
        """创建S0盒的一维查找表"""
        S0_table = [
            [0x3E, 0x72, 0x5B, 0x47, 0xCA, 0xE0, 0x00, 0x33, 0x04, 0xD1, 0x54, 0x98, 0x09, 0xB9, 0x6D, 0xCB],
            [0x7B, 0x1B, 0xF9, 0x32, 0xAF, 0x9D, 0x6A, 0xA5, 0xB8, 0x2D, 0xFC, 0x1D, 0x08, 0x53, 0x03, 0x90],
            [0x4D, 0x4E, 0x84, 0x99, 0xE4, 0xCE, 0xD9, 0x91, 0xDD, 0xB6, 0x85, 0x48, 0x8B, 0x29, 0x6E, 0xAC],
            [0xCD, 0xC1, 0xF8, 0x1E, 0x73, 0x43, 0x69, 0xC6, 0xB5, 0xBD, 0xFD, 0x39, 0x63, 0x20, 0xD4, 0x38],
            [0x76, 0x7D, 0xB2, 0xA7, 0xCF, 0xED, 0x57, 0xC5, 0xF3, 0x2C, 0xBB, 0x14, 0x21, 0x06, 0x55, 0x9B],
            [0xE3, 0xEF, 0x5E, 0x31, 0x4F, 0x7F, 0x5A, 0xA4, 0x0D, 0x82, 0x51, 0x49, 0x5F, 0xBA, 0x58, 0x1C],
            [0x4A, 0x16, 0xD5, 0x17, 0xA8, 0x92, 0x24, 0x1F, 0x8C, 0xFF, 0xD8, 0xAE, 0x2E, 0x01, 0xD3, 0xAD],
            [0x3B, 0x4B, 0xDA, 0x46, 0xEB, 0xC9, 0xDE, 0x9A, 0x8F, 0x87, 0xD7, 0x3A, 0x80, 0x6F, 0x2F, 0xC8],
            [0xB1, 0xB4, 0x37, 0xF7, 0x0A, 0x22, 0x13, 0x28, 0x7C, 0xCC, 0x3C, 0x89, 0xC7, 0xC3, 0x96, 0x56],
            [0x07, 0xBF, 0x7E, 0xF0, 0x0B, 0x2B, 0x97, 0x52, 0x35, 0x41, 0x79, 0x61, 0xA6, 0x4C, 0x10, 0xFE],
            [0xBC, 0x26, 0x95, 0x88, 0x8A, 0xB0, 0xA3, 0xFB, 0xC0, 0x18, 0x94, 0xF2, 0xE1, 0xE5, 0xE9, 0x5D],
            [0xD0, 0xDC, 0x11, 0x66, 0x64, 0x5C, 0xEC, 0x59, 0x42, 0x75, 0x12, 0xF5, 0x74, 0x9C, 0xAA, 0x23],
            [0x0E, 0x86, 0xAB, 0xBE, 0x2A, 0x02, 0xE7, 0x67, 0xE6, 0x44, 0xA2, 0x6C, 0xC2, 0x93, 0x9F, 0xF1],
            [0xF6, 0xFA, 0x36, 0xD2, 0x50, 0x68, 0x9E, 0x62, 0x71, 0x15, 0x3D, 0xD6, 0x40, 0xC4, 0xE2, 0x0F],
            [0x8E, 0x83, 0x77, 0x6B, 0x25, 0x05, 0x3F, 0x0C, 0x30, 0xEA, 0x70, 0xB7, 0xA1, 0xE8, 0xA9, 0x65],
            [0x8D, 0x27, 0x1A, 0xDB, 0x81, 0xB3, 0xA0, 0xF4, 0x45, 0x7A, 0x19, 0xDF, 0xEE, 0x78, 0x34, 0x60]
        ]
  
        s0_1d = [0] * 256
        for i in range(16):
            for j in range(16):
                s0_1d[i * 16 + j] = S0_table[i][j]
        return s0_1d
  
    def _create_s1(self):
        """创建S1盒的一维查找表"""
        S1_table = [
            [0x55, 0xC2, 0x63, 0x71, 0x3B, 0xC8, 0x47, 0x86, 0x9F, 0x3C, 0xDA, 0x5B, 0x29, 0xAA, 0xFD, 0x77],
            [0x8C, 0xC5, 0x94, 0x0C, 0xA6, 0x1A, 0x13, 0x00, 0xE3, 0xA8, 0x16, 0x72, 0x40, 0xF9, 0xF8, 0x42],
            [0x44, 0x26, 0x68, 0x96, 0x81, 0xD9, 0x45, 0x3E, 0x10, 0x76, 0xC6, 0xA7, 0x8B, 0x39, 0x43, 0xE1],
            [0x3A, 0xB5, 0x56, 0x2A, 0xC0, 0x6D, 0xB3, 0x05, 0x22, 0x66, 0xBF, 0xDC, 0x0B, 0xFA, 0x62, 0x48],
            [0xDD, 0x20, 0x11, 0x06, 0x36, 0xC9, 0xC1, 0xCF, 0xF6, 0x27, 0x52, 0xBB, 0x69, 0xF5, 0xD4, 0x87],
            [0x7F, 0x84, 0x4C, 0xD2, 0x9C, 0x57, 0xA4, 0xBC, 0x4F, 0x9A, 0xDF, 0xFE, 0xD6, 0x8D, 0x7A, 0xEB],
            [0x2B, 0x53, 0xD8, 0x5C, 0xA1, 0x14, 0x17, 0xFB, 0x23, 0xD5, 0x7D, 0x30, 0x67, 0x73, 0x08, 0x09],
            [0xEE, 0xB7, 0x70, 0x3F, 0x61, 0xB2, 0x19, 0x8E, 0x4E, 0xE5, 0x4B, 0x93, 0x8F, 0x5D, 0xDB, 0xA9],
            [0xAD, 0xF1, 0xAE, 0x2E, 0xCB, 0x0D, 0xFC, 0xF4, 0x2D, 0x46, 0x6E, 0x1D, 0x97, 0xE8, 0xD1, 0xE9],
            [0x4D, 0x37, 0xA5, 0x75, 0x5E, 0x83, 0x9E, 0xAB, 0x82, 0x9D, 0xB9, 0x1C, 0xE0, 0xCD, 0x49, 0x89],
            [0x01, 0xB6, 0xBD, 0x58, 0x24, 0xA2, 0x5F, 0x38, 0x78, 0x99, 0x15, 0x90, 0x50, 0xB8, 0x95, 0xE4],
            [0xD0, 0x91, 0xC7, 0xCE, 0xED, 0x0F, 0xB4, 0x6F, 0xA0, 0xCC, 0xF0, 0x02, 0x4A, 0x79, 0xC3, 0xDE],
            [0xA3, 0xEF, 0xEA, 0x51, 0xE6, 0x6B, 0x18, 0xEC, 0x1B, 0x2C, 0x80, 0xF7, 0x74, 0xE7, 0xFF, 0x21],
            [0x5A, 0x6A, 0x54, 0x1E, 0x41, 0x31, 0x92, 0x35, 0xC4, 0x33, 0x07, 0x0A, 0xBA, 0x7E, 0x0E, 0x34],
            [0x88, 0xB1, 0x98, 0x7C, 0xF3, 0x3D, 0x60, 0x6C, 0x7B, 0xCA, 0xD3, 0x1F, 0x32, 0x65, 0x04, 0x28],
            [0x64, 0xBE, 0x85, 0x9B, 0x2F, 0x59, 0x8A, 0xD7, 0xB0, 0x25, 0xAC, 0xAF, 0x12, 0x03, 0xE2, 0xF2]
        ]
  
        s1_1d = [0] * 256
        for i in range(16):
            for j in range(16):
                s1_1d[i * 16 + j] = S1_table[i][j]
        return s1_1d
  
    def sbox_32(self, X):
        """
        32位S盒变换
        :param X: 32位输入
        :return: 32位输出
        """
        # 将32位输入分解为4个8位字节
        x0 = (X >> 24) & 0xFF
        x1 = (X >> 16) & 0xFF
        x2 = (X >> 8) & 0xFF
        x3 = X & 0xFF
  
        # 分别应用S盒
        y0 = self.S0[x0]
        y1 = self.S1[x1]
        y2 = self.S0[x2]  # S2 = S0
        y3 = self.S1[x3]  # S3 = S1
  
        # 重新组合为32位输出
        Y = (y0 << 24) | (y1 << 16) | (y2 << 8) | y3
        return Y

############## 使用ZUC生成的密钥流加密 ##############
def zuc_encrypt(key, iv, data):
    """
    使用ZUC算法加密数据
    :param key: 128位密钥 (16字节)
    :param iv: 128位初始向量 (16字节)
    :param data: 要加密的数据 (字节串)
    :return: 加密后的数据 (字节串)
    """
    print("=== ZUC加密开始 ===")
  
    # 初始化ZUC算法
    zuc = ZUCAlgorithm(key, iv)
  
    # 执行初始化阶段
    zuc.initialization_phase()
  
    # 计算需要的密钥字数量
    data_len = len(data)
    key_words_needed = (data_len + 3) // 4  # 每个密钥字对应4字节数据
  
    # 生成密钥流
    keystream = zuc.generate_keystream(key_words_needed)
  
    # 将密钥流转换为字节流
    keystream_bytes = bytearray()
    for word in keystream:
        keystream_bytes.extend([
            (word >> 24) & 0xFF,
            (word >> 16) & 0xFF,
            (word >> 8) & 0xFF,
            word & 0xFF
        ])
  
    # 将数据与密钥流异或
    encrypted = bytearray()
    for i in range(data_len):
        encrypted.append(data[i] ^ keystream_bytes[i])
  
    print(f"加密完成: {len(data)}字节")
    print("=== ZUC加密结束 ===\n")
  
    return bytes(encrypted)

############## 使用ZUC解密生成的密钥流加密 ##############
def zuc_decrypt(key, iv, encrypted_data):
    """
    使用ZUC算法解密数据
    ZUC是对称算法，解密与加密过程相同 （对称加密）
    """
    return zuc_encrypt(key, iv, encrypted_data)


# main()
if __name__ == "__main__":
    print("ZUC算法测试")

    key = bytes([0x00] * 16)
    iv = bytes([0x00] * 16)
    data = b"Hello, ZUC Algorithm!"
  
    print("测试: 全0密钥和初始向量")
    encrypted = zuc_encrypt(key, iv, data)
    decrypted = zuc_decrypt(key, iv, encrypted)
  
    print(f"原始数据: {data}")
    print(f"加密数据: {encrypted.hex()}")
    print(f"解密数据: {decrypted}")
    print(f"加解密成功: {data == decrypted}\n")

预处理

在开始介绍算法之前，先来我们传入的参数是什么意思：

key = bytes([0x00] * 16)	# 密钥
iv = bytes([0x00] * 16)	# 向量
data = b"Hello, ZUC Algorithm!" # 待加密的内容

• 密钥：128位（也就是16字节）。核心参数，决定了加密系统的根本安全性。因为其从根本上决定了伪随机密钥流的“基座”或“种子模式”。不同的密钥会产生完全不同的、不相关的密钥流序列。需要严格保密
• IV（向量）：128位（也就是16字节）。密码学中存在一种 重放攻击（作者不懂，不过多介绍），而引入 向量可以确保密钥流的随机性与唯一性，防止 重放攻击。通常不需要保密，因为每次加密都应该引入一个完全不同、唯一的向量

IV（向量）与密钥协同工作，为每次加密都会生成一个独一无二的起始点。即使用相同的密钥，只要IV（向量）不同，ZUC算法产生的密钥流就会完全不同。这确保了即使加密了两段完全相同的明文，得到的密文也会截然不同。

• 待加密的内容：可以是任意、随机、完全无限制的一段数据。ZUC是一种流密钥，意味着生成的一个个bit的 流密钥，我们只需要生成与待加密数据对应长度的密钥字即可进行加密。

了解了这些以后，我们来看我们代码的主函数，在python中也就是：

# main()
if __name__ == "__main__":
    print("ZUC算法测试")

    key = bytes([0x00] * 16)
    iv = bytes([0x00] * 16)
    data = b"Hello, ZUC Algorithm!"
  
    print("测试: 全0密钥和初始向量")
    encrypted = zuc_encrypt(key, iv, data)
    decrypted = zuc_decrypt(key, iv, encrypted)
  
    print(f"原始数据: {data}")
    print(f"加密数据: {encrypted.hex()}")
    print(f"解密数据: {decrypted}")
    print(f"加解密成功: {data == decrypted}\n")

那么我们直接来看ZUC的加密函数：zuc_encrypt(key, iv, data)

（）def zuc_encrypt(key, iv, data):
    """
    :param key: 128位密钥 (16字节)
    :param iv: 128位初始向量 (16字节)
    :param data: 要加密的数据 (字节串)
    :return: 加密后的数据 (字节串)
    """
    print("=== ZUC加密开始 ===")
  
    # 初始化ZUC算法
    zuc = ZUCAlgorithm(key, iv)
  
    # 执行初始阶段（我更喜欢称之为预热阶段）
    zuc.initialization_phase()
  
    # 计算需要的密钥字数量
    data_len = len(data)
    key_words_needed = (data_len + 3) // 4  # 每个密钥字对应4字节数据
  
    # 生成密钥流
    keystream = zuc.generate_keystream(key_words_needed)
  
    # 将密钥流转换为字节流
    keystream_bytes = bytearray()
    for word in keystream:
        keystream_bytes.extend([
            (word >> 24) & 0xFF,
            (word >> 16) & 0xFF,
            (word >> 8) & 0xFF,
            word & 0xFF
        ])
  
    # 将数据与密钥流异或
    encrypted = bytearray()
    for i in range(data_len):
        encrypted.append(data[i] ^ keystream_bytes[i])
  
    print(f"加密完成: {len(data)}字节")
    print("=== ZUC加密结束 ===\n")
  
    return bytes(encrypted)

可以看到，整个加密函数一共分为这几步：

• ①将我们提供的参数，也就是将key、IV传入一个初始化函数
• ②加载算法的起步阶段函数，但是我更喜欢称其为“预热”阶段
• ③计算所需的密钥字数量，生成密钥流，也就是启动ZUC算法的工作模式
• ④最后将密钥流转换为字节流（其实也就是需要和数据的格式一致），将数据与密钥流异或，完成加密

其中前三部是我们要关注的重点，也就是密钥流是如何来的，最后的异或其实无关紧要

我们来一步步看下去

传参

先来看我们的key和iv被用来干什么了：

class ZUCAlgorithm:

    def __init__(self, key, iv):
        """
        :param key: 128位初始密钥 (16字节)
        :param iv: 128位初始向量 (16字节)
        """
        print("=== ZUC算法初始化开始 ===")
  
        # LFSR: 16个31位寄存器  
        self.LFSR = [0] * 16	# 可以先不管
  
        # 非线性函数F的记忆单元
        self.R1 = 0
        self.R2 = 0
  
        self.key = key
        self.iv = iv
  
        print(f"密钥: {key.hex()}")
        print(f"初始向量: {iv.hex()}")
  
        # 初始化常量
        self.d = self._init_d_constants()
        self.sbox = ZUCSBox()
  
        print("=== ZUC算法初始化完成 ===\n")
################## 下面的代码与接下来要展示的东西无关 ################

调用这个类会触发构造函数（__init__ 魔术方法），其主要干了这么几件事：

• 将key、iv传给类成员 ：self.key = key 、self.iv = iv
• 将R1、R2置零（先不管，后面介绍）
• 声明LFSR的16个31位寄存器，以数组实现（先不管，后面介绍）
• 调用了 _init_d_constants()、ZUCSBox()初始化（照样先不管，马上就知道用来干什么）

都是些初始化，由于其中参数我们很多都不认识，所以先不管

这里展示的主要原因是留个印象，接下来我们会一一介绍

接下来我们返回上一层，来看预热函数：initialization_phase()

def initialization_phase(self):

        print("=== 初始化步骤开始 ===")
  
        # (a) 密钥装入
        print("步骤(a): 密钥装入")
        self.key_load()
  
        # (b) 初始化R1和R2为0
        print("步骤(b): 初始化R1和R2为0")
        self.R1 = 0
        self.R2 = 0
  
        # (c) 重复执行32次
        print("步骤(c): 执行32轮初始化")
        for i in range(32):
            print(f"  第{i+1}轮初始化:")
  
            # 1) 比特重组
            X0, X1, X2, X3 = self.bit_reconstruction()
            print(f"    比特重组: X0={X0:08x}, X1={X1:08x}, X2={X2:08x}, X3={X3:08x}")
  
            # 2) 非线性函数F
            W = self.nonlinear_function_F(X0, X1, X2)
            print(f"    非线性函数F: W={W:08x}, R1={self.R1:08x}, R2={self.R2:08x}")
  
            # 3) 输出W (在初始化阶段通常不输出)
  
            # 4) LFSR初始化模式，输入W>>1 (取31位)
            u = W >> 1
            self.lfsr_initialization_mode(u)
            print(f"    LFSR更新: u={u:08x}")
  
        print("=== 初始化步骤完成 ===\n")

接着我们来看预处理阶段最重要的密钥装入部分，在算法标准结构图中，也就是将原本空的s0-s15装入内容：

密钥装入

先贴代码

def key_load(self):

    print("=== 密钥装入过程开始 ===")
  
    for i in range(16): # ①确保每个寄存器都包含了密钥、固定值和初始向量的信息
        # 提取密钥和初始向量的字节
        k_byte = self.key[i]
        iv_byte = self.iv[i]
  
        # s_i = k_i || d_i || iv_i
        # k_i: 8位, d_i: 15位, iv_i: 8位
        self.LFSR[i] = (k_byte << 23) | (self.d[i] << 8) | iv_byte
  
        print(f"LFSR[{i}] = {self.LFSR[i]:08x} (k={k_byte:02x}, d={self.d[i]:04x}, iv={iv_byte:02x})")
  
    print("=== 密钥装入过程完成 ===\n")

这里指的密钥装入，事实上指的是将key + iv 配合用于初始化 LFSR的16个寄存器，即s0-s15

简单介绍以下 LFSR是什么：全程“线性反馈移位寄存器”，一个会进行移位的寄存器，其输入由自身获得，可以产生“伪随机（最大周期是 2^n - 1）”的输出序列，密码学中它的作用是快速产生一个长周期的伪随机密钥流

具体 LFSR我们下面会介绍，这里要讲的是这段代码是如何将我们的key + iv装入这16个寄存器的：

• 进行16轮操作，每轮操作如下：
• ①遍历，从key和iv提取一个字节，分别记作k_i、iv_i
• ②第i个寄存器记作s_i
• ③将s_i 赋值为 ：k_i的后8位 + d_i的后15位（先别急马上介绍）+ iv_i的8位
• ④这样子每个s_i就是31位了

可以看到，我们传入的key并不是完全利用到了，而是只取其8位，配合一个15位的参数d_i以及iv中的8位，拼接成一个 8 + 15 + 8共31位的值

这里我们可以看到出现了一个奇怪的参数 ：d_i

它在前面被我们忽视了：_init_d_constants()

def _init_d_constants(self):
    """初始化15位常量d_i"""
    print("步骤: 初始化15位常量d_i")
    d_values = [
        0b100010011010111, 0b010011010111100, 0b110001001101011,
        0b001001101011110, 0b101011110001001, 0b011010111100010,
        0b111000100110101, 0b000100110101111, 0b100110101111000,
        0b010111100010011, 0b110101111000100, 0b001101011110001,
        0b101111000100110, 0b011110001001101, 0b111100010011010,
        0b100011110101100
    ]
    return d_values

d_i可以看到，它其实是一段段二进制参数，其作用是：通过将密钥（ki）、常数（di）和初始向量（ivi）连接起来，保证了即使密钥或初始向量部分相同，LFSR的初始状态也会因常数的引入而不同。这防止了初始状态全为零或其他弱状态，从而避免了密码分析中的弱点。

在ZUC算法中，di 是一组预定义的15位常数（即每个 di 占15位），用于LFSR的初始化。这些常数是ZUC标准的一部分，由算法设计者精心选择，以优化LFSR的统计特性。我们只需要记住：di是配合我们提供的key和iv使用、用于装填空的LFSR寄存器用的

我们还注意到，每个寄存器只取31位，其原因，作者这里也不完全理解（数学不好），贴上查到的解释：

• ZUC的LFSR不是工作在传统的基于异或的GF(2)上，而是工作在模素数 p = 2³¹ - 1 的有限域 GF(p) 上
• 这个素数 p 是一个 梅森素数 。在GF(p)上设计的LFSR，如果其反馈多项式是一个本原多项式，那么它能够达到的 最大周期是 p - 1 = 2³¹ - 2 。这是一个巨大的、已知的、且是可能达到的最大周期。
• 如果使用32位（2³²），那么模数将是2³²。在GF(2)上，基于异或的LFSR的最大周期是2³² - 1，这虽然也很大，但ZUC的设计者选择了GF(p)这条路径。

而key、iv各取8位的原因是将Key、IV和常数d高度混合混，使得分析密钥和输出序列之间的关系变得极其困难

总之，进行16轮这样的key、d、iv的混合后，我们就得到了16个已经“装满货物”的寄存器，到这里，我们提供的key与iv也就尽完它们的职责了，也就是完成密钥装入

initialization_phase()函数接下来还有一步：设置R1、R2为0，还是先跳过（或者直接去看 非线性函数F部分也可）

然后是开始进入到一个32次的循环，这也是ZUC算法的重点，但是我们先一步步介绍循环的函数到底是什么，再来说明为什么循环32次

线性反馈移位寄存器(LFSR)

虽然给的代码是 比特重组（BR）——> 非线性函数（F） ——> 线性反馈移位寄存器（LFSR），但是由于这个部分与后面两个部分有紧密关联，所以先提前给出

还记得我们前面说过：LFSR密码学中它的作用是快速产生一个长周期的伪随机密钥流，其生成的密钥流就是为后面进行混淆的对象，也就是说，你可以把 LFSR当作我们生成的ZUC密钥流的“种子算法”，负责维护算法的大部分内部状态。

伪随机的原因是其具有周期性，最大为 2^n - 1（原理可自己查查），但是我们设置16个31为LFSR意味着状态空间高达496位，在数学上足以抵抗暴力破解

那么它是如何长周期产生一个长周期的伪伪随机密钥流的呢？

我们结合一下算法标准结构图来看看其实际计算流程：

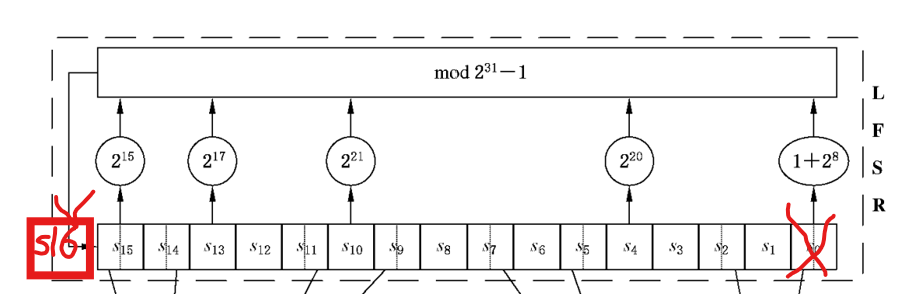
（简单处理了一下）

其逻辑就是：取s15、s13、s10、s4、s0这5个值，进行一堆运算之后，得到一个新值s16，并将s0踢出去，将得到的s16放到最后。

这个流程就像是我们砍竹子（比喻也许不够恰当），一根竹子一共16节（最多且必须），我们把最头部的一节砍了（丢掉s0），然后底部长出一根新节（生成s16）。这样子就能保证，整根竹子都处于最嫩的状态（一直在更新），且会一直保持生长（一直保持16节）

那么我们是如何得到这个新的竹节，也就是 s16的呢？

来看代码：lfsr_initialization_mode(u)

def lfsr_initialization_mode(self, u):
    """
    5.2.2 LFSR初始模式
    LFSR接收1个31比特字u的输入，更新寄存器
    """
    # (1) 计算v
    v = self.mod_231_1_mult(2**15, self.LFSR[15])
    v = self.mod_231_1_add(v, self.mod_231_1_mult(2**17, self.LFSR[13]))
    v = self.mod_231_1_add(v, self.mod_231_1_mult(2**21, self.LFSR[10]))
    v = self.mod_231_1_add(v, self.mod_231_1_mult(2**20, self.LFSR[4]))
    v = self.mod_231_1_add(v, self.mod_231_1_mult((1 + 2**8), self.LFSR[0]))
  
    # (2) 计算s16
    s16 = self.mod_231_1_add(v, u)
  
    # (3) 如果s16=0，则置s16=2^31-1
    if s16 == 0:
        s16 = 2**31 - 1
  
    # (4) 移位操作
    for i in range(15):
        self.LFSR[i] = self.LFSR[i + 1]
    self.LFSR[15] = s16
  
    return s16

但是，如果你先提前全部浏览整个文章，会发现还有个函数与LFSR有关：lfsr_work_mode(self)

def lfsr_work_mode(self):
    """
    5.2.3 LFSR工作模式
    LFSR无输入，直接更新寄存器
    """
    # (1) 计算s16
    s16 = self.mod_231_1_mult(2**15, self.LFSR[15])
    s16 = self.mod_231_1_add(s16, self.mod_231_1_mult(2**17, self.LFSR[13]))
    s16 = self.mod_231_1_add(s16, self.mod_231_1_mult(2**21, self.LFSR[10]))
    s16 = self.mod_231_1_add(s16, self.mod_231_1_mult(2**20, self.LFSR[4]))
    s16 = self.mod_231_1_add(s16, self.mod_231_1_mult((1 + 2**8), self.LFSR[0]))
  
    # (2) 如果s16=0，则置s16=2^31-1
    if s16 == 0:
        s16 = 2**31 - 1
  
    # (3) 移位操作
    for i in range(15):
        self.LFSR[i] = self.LFSR[i + 1]
    self.LFSR[15] = s16
  
    return s16

s s16有两种生成办法？！这实际上这告诉我们：LFSR有两个状态。为什么？

这实际上就是ZUC算法的核心设计：这两种模式的存在是为了解决一个根本矛盾：如何从一个确定的密钥和IV出发，最终生成一个随机、不可预测且“高效生成”的密钥流？答案就是加入“混淆与扩散”。

• 密钥装填：实现了从一个密钥（key）和向量（IV）出发
• 初始模式 ：目的是 “混淆和扩散” ，将算法内部状态“打乱”，使其达到一个充分随机的起始点，看不出内部状态与我们的IV、密钥的关系（注意只是起始点，还是不能直接作为密码使用！后面会解释）

• 工作模式 ：目的是 “高效生成” ,可以快速得到安全可靠的密钥流。

我们来一步步介绍这两个函数（状态）

初始模式

首先来看 lfsr_initialization_mode(u)，也就是 LFSR初始模式：

我们在前面已经进行过 密钥装入，也就是把IV和key还有常数d装进16个31位空的寄存器里面了，接下来为了实现我们“看不出内部状态与我们的IV、密钥的关系”的目标，就需要打乱现在16个31位寄存器的关系

可以看到，初始模式生成 s16的过程需要提供一个31位的输入 u，其来源可以在 initialization_phase(self)函数中看到，来自 非线性函数F的运行结果，我们后面再讲这一步，这里我们就把 u当作一个安全的、可靠的“搅屎棍”

先来看我们计算s16的代码

# (1) 计算v
v = self.mod_231_1_mult(2**15, self.LFSR[15])
v = self.mod_231_1_add(v, self.mod_231_1_mult(2**17, self.LFSR[13]))
v = self.mod_231_1_add(v, self.mod_231_1_mult(2**21, self.LFSR[10]))
v = self.mod_231_1_add(v, self.mod_231_1_mult(2**20, self.LFSR[4]))
v = self.mod_231_1_add(v, self.mod_231_1_mult((1 + 2**8), self.LFSR[0]))
  
# (2) 计算s16
s16 = self.mod_231_1_add(v, u)

可以看到LFSR的初始模式，计算中间值 v与 S16时，分别调用了两个函数： mod_231_1_mult(self, a, b)、mod_231_1_add(self, a, b)

def mod_231_1_add(self, a, b):
    """
    模2^31-1加法实现
    """
    result = a + b
    # 模2^31-1运算
    result = (result & 0x7FFFFFFF) + (result >> 31)
    return result
  
def mod_231_1_mult(self, a, b):
    """
    模2^31-1乘法实现
    """
    # 简单的模乘法实现
    # 在实际应用中可以使用更高效的实现
    return (a * b) % (2**31 - 1)

这两个函数其实就是我们结构图中对 s15它们进行的运算，本质是是一种 模运算（记住如何实现就行）

来介绍一下 v：LFSR线性特性的集中体现：

• 线性混合 ：v 是由 LFSR中 5个特定寄存器 s15, s13, s10, s4, s0通过线性组合计算得出的。
• 扩散作用 ：这些寄存器在 LFSR中分布较广（索引0,4,10,13,15），确保了 LFSR状态的广泛参与。
• 数学基础 ：计算基于 Galois域 GF(2^31-1) 上的运算（与31位寄存器对应），保证了LFSR能达到最大周期。

没事，我也看不懂这里面的数学逻辑，但是，简单说：v 代表了LFSR"本来应该"按照线性规则生成的下一个状态。

初始模式最关键的是 s16的得到方式，将前面得到的 线性的v与我们给的 非线性的u进行了 模加法，然后丢掉 LFSR最前面的一个值 s0，将 s16放到最后，这意味着，相当于在 LFSR的线性序列中植入了非线性基因

举个例子：

对于一个一般的可破解 LFSR序列在程序的眼里长这样: a-b-c-d-e-f-1-2-3-4-5-6

在加入了 s16整个非线性基因后，可以长这样 b-c-d-e-f-1-2-3-4-5-6-🔣

而这个🔣即使与前一个状态：a-b-c-d-e-f-1-2-3-4-5-6有密切关系，但是就算你是计算机本体都看不出这玩意到底和我们的密钥、IV有半毛钱关系，实现了我们“扩散与混淆”的目的

当然简单一轮是完全不够的， initialization_phase(self)函数中进行了32轮这样的****非线性基因植入，足够达到了一个高度随机化的"混沌"状态.

工作模式

达到我们要的混沌状态之后，就不需要我们继续提供 非线性的u了，之后只需要让它愉快地产生随机密钥流即可，在代码中，我们可以看到 这个模式下的 s16算法与初始模式的 v一致，即：在我们初始模式中，生成 v的算法，就是工作模式生成 s16的算法，就不过多介绍了

为什么不能直接作为密钥使用

但是！正如我们代码中看到的，虽然 key、IV和 LFSR生成的密钥流序列的 内部关系是非线性的，但是 LFSR生成的密钥流的 外部关系是线性的，这意味着攻击者只需要截获一小段输出序列（2n个比特），就可以通过解一个线性方程组（例如使用 Berlekamp-Massey算法）轻松地推算出 LFSR的反馈多项式和整个后续输出序列，从而完全破解加密。

所以，不能直接将得到的 LFSR密钥流作为真正的密钥流使用，那该怎么办呢？接下来我们要介绍的 比特重组和 非线性函数F就是为了解决这个问题而设计的

比特重组(BR)

这一步代码非常简单，来看 比特重组的函数：bit_reconstruction()

def bit_reconstruction(self):
    """
    比特重组(BR)
    从LFSR寄存器中重组4个32位字X0, X1, X2, X3
    """
    # 提取LFSR寄存器的高16位和低16位
    s15H = (self.LFSR[15] >> 15) & 0xFFFF  # s15的高16位
    s14L = self.LFSR[14] & 0x7FFF          # s14的低15位
    s11H = (self.LFSR[11] >> 15) & 0xFFFF  # s11的高16位
    s9L = self.LFSR[9] & 0x7FFF            # s9的低15位
    s7H = (self.LFSR[7] >> 15) & 0xFFFF    # s7的高16位
    s5L = self.LFSR[5] & 0x7FFF            # s5的低15位
    s2H = (self.LFSR[2] >> 15) & 0xFFFF    # s2的高16位
    s0L = self.LFSR[0] & 0x7FFF            # s0的低15位
  
    # 重组32位字
    X0 = (s15H << 16) | s14L
    X1 = (s11H << 16) | s9L
    X2 = (s7H << 16) | s5L
    X3 = (s2H << 16) | s0L
  
    return X0, X1, X2, X3

比特重组（BR） 是ZUC算法中一个非常精巧且关键的设计，它充当了 LFSR（线性部分）和 非线性函数F（非线性部分）之间的"桥梁"。简单来说，比特重组做了一件看似简单但至关重要的事情：它从 LFSR的16个寄存器中，有选择地、按特定规则抽取一些位，然后重新打包成4个32位的字（X0, X1, X2, X3），供后续步骤（非线性函数F）使用

具体来说，其抽取的寄存器、每个寄存器抽取的位是固定的：

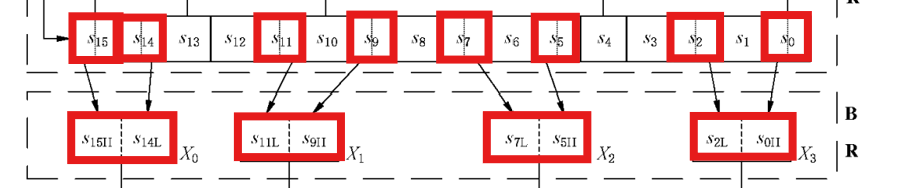
由于 LFSR的更新是“去头填尾”，相邻寄存器存在强关联，而 比特重组以不连续、广泛的方式去抽值，可以去除这种强关联，达到扩散的目的

而 比特重组返回的结果，4个32位字 X0, X1, X2, X3中，只有 X0, X1, X2 被送入 非线性函数F 当中，而 X3将会与 非线性函数F得到的 w进行异或，得到我们用来进行 LFSR的初始模式的 u，这样设计即实现了非线性，又保证了效率

知道了 比特重组的作用后，就可以看整个ZUC算法最复杂的一部分——非线性函数F了

非线性函数F

非线性函数F 是ZUC算法的安全核心，它负责将LFSR产生的 线性密钥流 转换为 非线性密钥流。让我们先看看它的代码：

def nonlinear_function_F(self, X0, X1, X2):
    """
    输入: X0, X1, X2 (32位字)
    输出: W (32位字)
    """
    # (1) W = (X0 ⊕ R1) + R2 mod 2^32
    W = ((X0 ^ self.R1) + self.R2) & 0xFFFFFFFF
  
    # (2) W1 = R1 + X1 mod 2^32
    W1 = (self.R1 + X1) & 0xFFFFFFFF
  
    # (3) W2 = R2 ⊕ X2
    W2 = self.R2 ^ X2
  
    # (4) R1 = S[L1(W1H || W2L)]
    W1H = (W1 >> 16) & 0xFFFF  # W1的高16位
    W2L = W2 & 0xFFFF          # W2的低16位
    R1_input = (W1H << 16) | W2L
    self.R1 = self.sbox.sbox_32(self.linear_transform_L1(R1_input))
  
    # (5) R2 = S[L2(W2H || W1L)]
    W2H = (W2 >> 16) & 0xFFFF  # W2的高16位
    W1L = W1 & 0xFFFF          # W1的低16位
    R2_input = (W2H << 16) | W1L
    self.R2 = self.sbox.sbox_32(self.linear_transform_L2(R2_input))
  
    return W

可以看到，其所用参数就是我们 比特重组一步得到的 X0、X1、X2

而返回的输出 W，实际上在该函数开头通过 W = (X0 ⊕ R1) + R2 mod 2^32这段代码就已经计算完毕了，那么后面一大段函数用来干什么呢？

而其中所需用到 R1、R2两个前面提到过的参数与 sbox_32(self, X)、linear_transform_L1(self, X)、linear_transform_L2(self, X)这三个函数又是什么呢？

记忆单元R1、R2

我们先来介绍 R1、R2这两个参数到底是什么：在ZUC算法的文档中，R1和R2被称为 32位记忆单元 。它们本质上就是两个32位的寄存器，在算法运行过程中会不断地被更新。同时保持非线性关系

正如其名字一样，它们两的作用是“记忆”，说起来有点抽象，我们先来思考这么一个问题：

• 如果每一轮产生的密钥流都只依赖于当前 LFSR的状态，那么 密钥流之间的关系就是相互独立的。攻击者可以孤立地分析每一段 密钥流（这里一段 密钥流实际上就是一次 LFSR运算生成的新31位数据）。
• 这意味着，攻击者截取到的密钥流片段对攻击来说是有意义的（具体多少没细研究）
• 如何在不断生成的一段段密钥流中，建立起联系，使得攻击者即使拿到其中一个片段都没有用呢？

设计者的解决方案是：引入 R1、R2这两个“记忆单元”，“记住”当前的 密钥流状态，让它们两加入到生成新的密钥流过程中。意思是：在 LFSR的第 n轮的计算中，此时 R1、R2它们的状态是第 n-1轮计算的结果，并且，由于迭代，当前的 R1、R2包括了过去所有轮次的“历史信息”，更准确地说，此时 LFSR的第 n轮的计算，与前 n-1轮都有关系

这使得 密钥流不再是一个独立的序列，而是一个连续的、前后高度关联的数据流。第100个 密钥字依赖于第99个，第99个依赖于第98个……一直回溯到初始化阶段。这极大地增加了密码分析的难度。

回到我们开头的看到的ZUC算法初始化函数，由于我们一开始并没有进行过 LFSR运算，所以开始一要将 R1、R2置0

然后回到 非线性函数F，我们已经知道了 R1、R2的作用了，所以我们也能理解 w的结构图中的生成是如何而来的了:

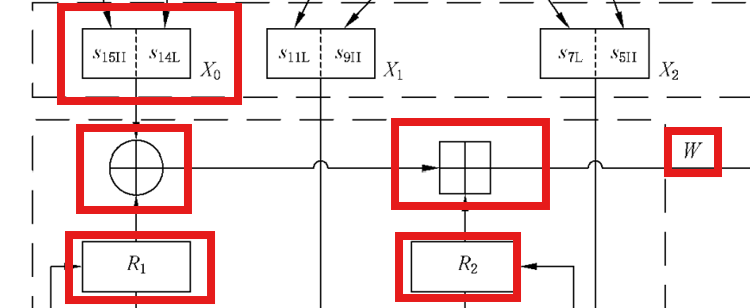
即↓

# (1) W = (X0 ⊕ R1) + R2 mod 2^32
W = ((X0 ^ self.R1) + self.R2) & 0xFFFFFFFF

这里就体现了后面生成的密钥流是与前面生成的密钥流有强联系的。

知道了 R1、R2的作用后，我们来来看看更新的 R1、R2的算法到底是什么：

为了方便理解接下来个个函数的关系与顺序，先奉上结构图（稍微处理了一下）

...
self.R1 = self.sbox.sbox_32(self.linear_transform_L1(R1_input))
self.R2 = self.sbox.sbox_32(self.linear_transform_L2(R2_input))
...

Sbox

按照图中标号顺序，我按照倒序的方法来介绍 R1、R2的更新过程。

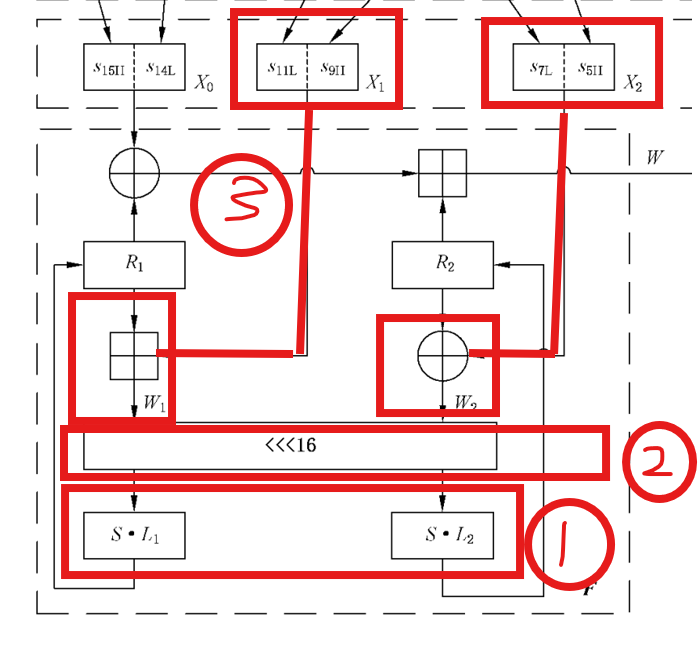
首先我们来看整个代码最核心的部分——非线性的Sbox。我们在前面提到一个类 ZUCSBox()，其构造函数长这样:

def __init__(self):
    print("初始化ZUC S盒...")
    self.S0 = self._create_s0()
    self.S1 = self._create_s1()

def _create_s0(self):
    """创建S0盒的一维查找表"""
    S0_table = [
        [0x3E, 0x72, 0x5B, 0x47, 0xCA, 0xE0, 0x00, 0x33, 0x04, 0xD1, 0x54, 0x98, 0x09, 0xB9, 0x6D, 0xCB],
        [0x7B, 0x1B, 0xF9, 0x32, 0xAF, 0x9D, 0x6A, 0xA5, 0xB8, 0x2D, 0xFC, 0x1D, 0x08, 0x53, 0x03, 0x90],
        [0x4D, 0x4E, 0x84, 0x99, 0xE4, 0xCE, 0xD9, 0x91, 0xDD, 0xB6, 0x85, 0x48, 0x8B, 0x29, 0x6E, 0xAC],
        [0xCD, 0xC1, 0xF8, 0x1E, 0x73, 0x43, 0x69, 0xC6, 0xB5, 0xBD, 0xFD, 0x39, 0x63, 0x20, 0xD4, 0x38],
        [0x76, 0x7D, 0xB2, 0xA7, 0xCF, 0xED, 0x57, 0xC5, 0xF3, 0x2C, 0xBB, 0x14, 0x21, 0x06, 0x55, 0x9B],
        [0xE3, 0xEF, 0x5E, 0x31, 0x4F, 0x7F, 0x5A, 0xA4, 0x0D, 0x82, 0x51, 0x49, 0x5F, 0xBA, 0x58, 0x1C],
        [0x4A, 0x16, 0xD5, 0x17, 0xA8, 0x92, 0x24, 0x1F, 0x8C, 0xFF, 0xD8, 0xAE, 0x2E, 0x01, 0xD3, 0xAD],
        [0x3B, 0x4B, 0xDA, 0x46, 0xEB, 0xC9, 0xDE, 0x9A, 0x8F, 0x87, 0xD7, 0x3A, 0x80, 0x6F, 0x2F, 0xC8],
        [0xB1, 0xB4, 0x37, 0xF7, 0x0A, 0x22, 0x13, 0x28, 0x7C, 0xCC, 0x3C, 0x89, 0xC7, 0xC3, 0x96, 0x56],
        [0x07, 0xBF, 0x7E, 0xF0, 0x0B, 0x2B, 0x97, 0x52, 0x35, 0x41, 0x79, 0x61, 0xA6, 0x4C, 0x10, 0xFE],
        [0xBC, 0x26, 0x95, 0x88, 0x8A, 0xB0, 0xA3, 0xFB, 0xC0, 0x18, 0x94, 0xF2, 0xE1, 0xE5, 0xE9, 0x5D],
        [0xD0, 0xDC, 0x11, 0x66, 0x64, 0x5C, 0xEC, 0x59, 0x42, 0x75, 0x12, 0xF5, 0x74, 0x9C, 0xAA, 0x23],
        [0x0E, 0x86, 0xAB, 0xBE, 0x2A, 0x02, 0xE7, 0x67, 0xE6, 0x44, 0xA2, 0x6C, 0xC2, 0x93, 0x9F, 0xF1],
        [0xF6, 0xFA, 0x36, 0xD2, 0x50, 0x68, 0x9E, 0x62, 0x71, 0x15, 0x3D, 0xD6, 0x40, 0xC4, 0xE2, 0x0F],
        [0x8E, 0x83, 0x77, 0x6B, 0x25, 0x05, 0x3F, 0x0C, 0x30, 0xEA, 0x70, 0xB7, 0xA1, 0xE8, 0xA9, 0x65],
        [0x8D, 0x27, 0x1A, 0xDB, 0x81, 0xB3, 0xA0, 0xF4, 0x45, 0x7A, 0x19, 0xDF, 0xEE, 0x78, 0x34, 0x60]
    ]
  
    s0_1d = [0] * 256
    for i in range(16):
        for j in range(16):
            s0_1d[i * 16 + j] = S0_table[i][j]
    return s0_1d

S0和 S1是两个精心设计的“输入8位，输出8位”的非线性查找表，简称 Sbox，但是，我们在上面代码可以看见，这个 Sbox一共有256个8位（两个16进制）值，如何实现的**“输入8位，输出8位”**呢？

其实，在 sbox.sbox_32(self, X)函数中就已经展示了查找的方法：

def sbox_32(self, X):
    """
    :param X: 32位输入
    :return: 32位输出
    """
    # 将32位输入分解为4个8位字节
    x0 = (X >> 24) & 0xFF
    x1 = (X >> 16) & 0xFF
    x2 = (X >> 8) & 0xFF
    x3 = X & 0xFF
  
    # 分别应用S盒
    y0 = self.S0[x0]
    y1 = self.S1[x1]
    y2 = self.S0[x2]  # S2 = S0
    y3 = self.S1[x3]  # S3 = S1
  
    # 重新组合为32位输出
    Y = (y0 << 24) | (y1 << 16) | (y2 << 8) | y3
    return Y

这个函数接受了一个 32位x，然后，将其分为4个8位的值，即一个2位16进制数（形如0xFF）,将其作为索引直接取 Sbox中的对应的值（也是8位），最后将得到的4个对应得8位值拼接为一个32位值

这里不难看出，8位的值作为索引共有2^8=256种情况，所以是256个8位值

而有两个 Sbox的原因，主要有三：

• 如果只用一个 Sbox，算法中会出现很多的对称性和重复模式。交替使用 S0和 S1打破了这种对称性，增加了算法的复杂性。
• 两个不同的 Sbox意味着攻击者需要同时分析两个独立的非线性系统，而不是一个。这样可以平方级地增加了代数攻击的难度。
• 不同的 Sbox减少了出现固定点（如 S(x) = x）和其他简单代数关系的概率。

顺带一提，为什么是8位？解释有很多，不过最好的记忆方法是：

• 8位（其实就算1字节）是现代计算机体系结构的基本处理单元。

由于本身 Sbox是 非线性的，于是有了以下 非线性传递链（以下参数都是前面出现过的）：Sbox -> R1/R2 -> w -> u -> LFSR生成的密钥流 -> ZUC生成的密钥流

总而言之，新 R1、R2的值就是通过传入 32位x作为索引，在 Sbox中查找对应的值得到的，那么，这个 32位x又是怎么来的呢？

线性变换

还是刚刚那个函数:

...
self.R1 = self.sbox.sbox_32(self.linear_transform_L1(R1_input))
self.R2 = self.sbox.sbox_32(self.linear_transform_L2(R2_input))
...

可以看到我们传入的 32位x的参数实际上是另两个函数的计算结果:linear_transform_L1(self, X)、linear_transform_L2(self, X)：

def linear_transform_L1(self, X):
    """
    线性变换L1
    L1(X) = X ⊕ (X <<< 2) ⊕ (X <<< 10) ⊕ (X <<< 18) ⊕ (X <<< 24)
    """
    def rotate_left_32(x, n):
        """32位循环左移"""
        return ((x << n) | (x >> (32 - n))) & 0xFFFFFFFF
  
    result = X
    result ^= rotate_left_32(X, 2)
    result ^= rotate_left_32(X, 10)
    result ^= rotate_left_32(X, 18)
    result ^= rotate_left_32(X, 24)
  
    return result & 0xFFFFFFFF
  
def linear_transform_L2(self, X):
    """
    线性变换L2
    L2(X) = X ⊕ (X <<< 8) ⊕ (X <<< 14) ⊕ (X <<< 22) ⊕ (X <<< 30)
    """
    def rotate_left_32(x, n):
        """32位循环左移"""
        return ((x << n) | (x >> (32 - n))) & 0xFFFFFFFF
  
    result = X
    result ^= rotate_left_32(X, 8)
    result ^= rotate_left_32(X, 14)
    result ^= rotate_left_32(X, 22)
    result ^= rotate_left_32(X, 30)
  
    return result & 0xFFFFFFFF

这两个函数称之为 线性变换，其最重要的功能即是实现“扩散”，简单来说，经过这么一个 线性变换操作，在 密钥流中，只要我们改动小小一个bit，就会影响输出中多个、看似不相关的bit，这极大确保了 整体密钥流的安全性

那么为什么会有两个 线性变换算法呢？粗俗点讲，这两个 线性变换的扩散程度不一样，使得攻击会更复杂，且攻击者还需猜测用的那种变换，增强安全性

虽然两个函数看起来代码很长，但是数学公式很好理解：L1(X) = X ⊕ (X <<< 2) ⊕ (X <<< 10) ⊕ (X <<< 18) ⊕ (X <<< 24)、L2(X) = X ⊕ (X <<< 8) ⊕ (X <<< 14) ⊕ (X <<< 22) ⊕ (X <<< 30)

对我们来说用代码实现还是很好理解的

交叉重组

最后，我们来看看是谁被进行了 线性变换，也就是 R1_input，来看看它是如何得到的

# W1 = R1 + X1 mod 2^32
W1 = (self.R1 + X1) & 0xFFFFFFFF
  
# W2 = R2 ⊕ X2
W2 = self.R2 ^ X2
  
W1H = (W1 >> 16) & 0xFFFF  # W1的高16位
W2L = W2 & 0xFFFF          # W2的低16位

R1_input = (W1H << 16) | W2L

self.R1 = self.sbox.sbox_32(self.linear_transform_L1(R1_input))

可以看到，在我们进行 线性变换之前，还将 R1、R2处理了一下，这一步叫做 交叉重组，其思路也简单，就是将 R1、R2，配合我们 比特重组得到的 X1、X2进行重新排列组合，这样做的目的也是我们一直在做的：加入“扩散”。将 R1、R2混合在一起，这样这两个参数的内在关系也不再是孤立的了，这样攻击者光有其中一个参数也不足以造成一次有效攻击

其数学逻辑看代码就很好理解了，就不做过多介绍到目前为止，我们就介绍完了 非线性函数F的所有关键操作了，但是由于我们是倒着讲的，所有这里我们重新梳理以下真正的操作：生成新w -> 将R1、R2交叉重组 -> 线性变换 -> Sbox查表

经历了这么复杂的一个过程，我们就能将我们从 LFSR中生成的密钥流进行“扩散与混淆”，保证了密码的安全性，这一个个经过“扩散与混淆的”密钥流，才能够真正作为我们去可靠使用的密钥去加密数据

小梳理

到这里，我们终于看完了初始化函数：zuc.initialization_phase()，回顾一下我们干了什么：

• 首先，我们看到开始会初始化一堆我们后面将会用到的参数，包括 R1、R2、Sbox填充等
• 其次，我们理解了我们传入的参数 key、IV的作用 —— 用于填充空的16个31位寄存器（LFSR）
• 之后，我们进行了32轮如下操作，其中真正的目的是完成 LFSR的初始模式，就是要将 key、IV完全混合在我们的 LFSR中，即进行 LFSR内部关系的“扩散与混淆”
• 第一步，我们看到，进行了 比特重组，也就是取 LFSR中的几个值去做混合，为接下来的 非线性函数F做预处理工作
• 第二步，我们把处理过的参数 V0....V3交给了 非线性函数F，其进行了 生成新w -> 将R1、R2交叉重组 -> 线性变换 -> Sbox查表 等操作后，得到了下一次要用的 R1、R2，以及处理好的 w，对 32位的w去除1位，就得到了我们要加入 LFSR的 u
• 第三步，我们将生成的 u给加入到新的 LFSR中。如此进行32轮，就再也看不出当前 LFSR的 密钥流与我们初始 key、IV的关系了

加密解密

接着我们来看接下来的关键函数：keystream=zuc.generate_keystream(key_words_needed)

def generate_keystream(self, L):
    """
    5.6.3 工作步骤
    生成L个32位密钥字
    :param L: 需要生成的密钥字数量
    :return: 密钥字列表
    """
    print("=== 工作步骤开始 ===")
    print(f"目标: 生成{L}个32位密钥字")
  
    keystream = []
  
    # (a) 执行一次工作阶段初始化
    print("步骤(a): 工作阶段初始化")
    X0, X1, X2, X3 = self.bit_reconstruction()
    print(f"  比特重组: X0={X0:08x}, X1={X1:08x}, X2={X2:08x}, X3={X3:08x}")
  
    self.nonlinear_function_F(X0, X1, X2)
    print(f"  非线性函数F: R1={self.R1:08x}, R2={self.R2:08x}")
  
    self.lfsr_work_mode()
    print("  LFSR工作模式更新完成")  
    # (b) 重复计算L次
    print(f"步骤(b): 生成{L}个密钥字")
    for i in range(L):
        print(f"  第{i+1}个密钥字生成:")
  
        # 1) 比特重组
        X0, X1, X2, X3 = self.bit_reconstruction()
        print(f"    比特重组: X0={X0:08x}, X1={X1:08x}, X2={X2:08x}, X3={X3:08x}")
  
        # 2) Z = F(X0,X1,X2) ⊕ X3
        F_output = self.nonlinear_function_F(X0, X1, X2)
        Z = F_output ^ X3
        print(f"    密钥字计算: F={F_output:08x}, Z=F⊕X3={Z:08x}")
  
        # 3) 输出密钥字Z
        keystream.append(Z)
  
        # 4) LFSR工作模式
        self.lfsr_work_mode()
        print(f"    LFSR工作模式更新完成")
  
    print("=== 工作步骤完成 ===\n")
    return keystream

这里有一个疑问点：为什么还要进行一次工作阶段初始化？

其实很简单：我们前面进行 比特重组+非线性函数F生成的值，最后都加入到 LFSR中了，也就是说，这些 密钥流字都是“非线性改造过的”，但是，在工作模式下的 LFSR，我们要的是“纯线性”的 密钥流字，所以，我们需要进行一次工作初始化，即把第一次生成的 密钥流字给“丢弃了”

当然另一种方便记忆的解释是：好比汽车发动，你得先开启引擎让他开一会看看正不正常运行

之后，我们就可以确保接下俩的 LFSR生成的密钥流之间是线性的，但是！是线性的，也就意味着密钥流之间是孤立的、密钥流也是不安全的，总而言之，其生成的密钥流不能直接作为密码

所以，我们还要对 LFSR生成的密钥流进行 比特重组+线性变换，也就是在进行一次“扩散与混淆”。这一步就是去除了 密钥流之间的外部线性关系

现在，只要我们按照给出待加密数据的长度，生成相应长度的密钥流，然后进行简单的操作：encrypted.append(data[i] ^ keystream_bytes[i])，就完成了加密操作了

上面这步可以看出，密文 = 密钥 ^ 明文，也就是说，ZUC密码是对称密码，所以，解密方式就算把密文当作明文丢进去，按照原来的 key、IV再次运行一次加密即可